A friend of mine has started to dabble in C# and he was surprised that there doesn’t seem to be an equivalent to the Python Combinations library. To be honest its something that I didn’t really know I was missing and my first thought was that its a simple enough problem to solve. But when I started trying to solve it, it turned out that I was very wrong.
To give the context, this is an example of what he was trying to do:
Output
The output is a set of unordered combinations, each of size 2.
An important metric in this calculation is performance. The python the function is impressively quick even with large sets. To solve this and to understand the performance I created a solution with a test project and a benchmark project. You can track my source code in this repo.
My first attempt to solve this was to use dynamic programming and recursion. The idea is to recursively split the array into smaller arrays and at the lowest level just to add small arrays of the configured size to a bag to ensure uniqueness. I created a class that a HashSet would treat a list of ints in an unordered manner.
private class Combination
{
public List<int> Data { get; private set; }
public Combination(IEnumerable<int> nums)
{
Data = nums.OrderBy(n=>n).ToList();
}
public override int GetHashCode()
{
int hashcode = 0;
unchecked
{
foreach (int num in Data)
{
hashcode += num.GetHashCode();
}
return hashcode;
}
}
public override bool Equals(object obj)
{
Combination other = obj as Combination;
return other != null && Data.SequenceEqual(other.Data);
}
}
Using this class, a HashSet would treat [1,2] and [2,1] as equal.
This is my recursive method to solve the problem.
public List<List<int>> SolveRecursive(List<int> nums, int size)
{
if (size > nums.Count)
{
return new List<List<int>> { nums };
}
var all = new List<List<int>>();
RecursiveInner(nums, size, new HashSet<Combination>(), all);
return all;
}
private void RecursiveInner(IEnumerable<int> nums, int size, HashSet<Combination> unique, List<List<int>> allCombinations)
{
if (nums.Count() == size)
{
var combination = new Combination(nums);
if (unique.Add(combination))
{
allCombinations.Add(combination.Data);
}
}
if (nums.Count() > size)
{
for (int i = 0; i < nums.Count(); i++)
{
var numsLessI = Enumerable.Concat(nums.Take(i), nums.Skip(i + 1).Take(nums.Count())).ToArray();
RecursiveInner(numsLessI, size, unique, allCombinations);
}
}
}
I will admit it! I have a soft spot for a recursive function. The problem with recursive functions is that when its comes to performance, they can be really poor. When running this function on my laptop, this functions started to get unusable when nums had 11 elements and size is 4. One problem with such a concise implementation is that its not that apparent on how to make it faster.
To get better performance, sometimes you have to start right back at the beginning and hope you find a better option. Thinking about it, if I was going to do this by hand, I would start enumerating through all possible combinations by flipping one index at a time.
Taking that idea further, I wrote a function that would enumerator an array from right to left and return a unique set of indexes.
public IEnumerable<List<int>> GenerateIndexes(int maxNum, int combSize)
{
var unique = new HashSet<Combination>();
var indexes = new int[combSize];
var mainIndex = combSize - 1;
int incIndex = mainIndex;
while (indexes.Any(i=>i< maxNum))
{
if(indexes[incIndex] < maxNum)
{
int i = combSize - 1;
while (indexes[i] == maxNum && i >= 0)
{
indexes[i] = 0;
incIndex = i;
i--;
}
indexes[i]++;
if(indexes.Distinct().Count() == combSize)
{
unique.Add(new Combination(indexes));
}
}
else
{
while(indexes[incIndex] >= maxNum && incIndex >=0)
{
incIndex--;
}
indexes[incIndex]++;
int i = combSize - 1;
while (i> incIndex)
{
indexes[i] = 0;
i--;
}
if (indexes.Distinct().Count() == combSize)
{
unique.Add(new Combination(indexes));
}
incIndex = combSize - 1;
if (incIndex < mainIndex)
{
mainIndex = incIndex;
}
}
}
return unique.Select(c => c.Data).ToList();
}
While this isn’t my most maintainable method, the tests pass. Ship it!
Now that I can generate a unique combination of indexes then its a pretty simple problem to solve.
public List<List<int>> SolveWithGenerator(List<int> nums, int size)
{
if (size > nums.Count)
{
return new List<List<int>> { nums };
}
var all = new List<List<int>>();
foreach(var indexCombination in GenerateIndexes(nums.Count - 1, size))
{
all.Add(indexCombination.Select(i => nums[i]).ToList());
}
return all;
}
Based my tests, both of these methods give the same result and so now it comes down to performance. Is it worth me throwing my fancy recursive function away for this complex index generator implementation? The only way to know is to measure. This is where BenchmarkDotnet shines. I created a 30 line class that scientifically measures both speed and memory of both methods with different inputs.
[MemoryDiagnoser]
public class AllCombinationsBenchmarks
{
private Combinations.AllCombinations allCombinations = new Combinations.AllCombinations();
[Params(2, 4)]
public int Size { get; set; }
[ParamsSource(nameof(ValuesForNum))]
public List<int> Num { get; set; }
public List<List<int>> ValuesForNum => new List<List<int>> {
Enumerable.Range(1,4).ToList(),
Enumerable.Range(1,7).ToList(),
Enumerable.Range(1,11).ToList(),
};
[Benchmark]
public void Recursive()
{
allCombinations.SolveRecursive(Num, Size);
}
[Benchmark]
public void Generator()
{
allCombinations.SolveWithGenerator(Num, Size);
}
}
Running these benchmarks gives the following output.
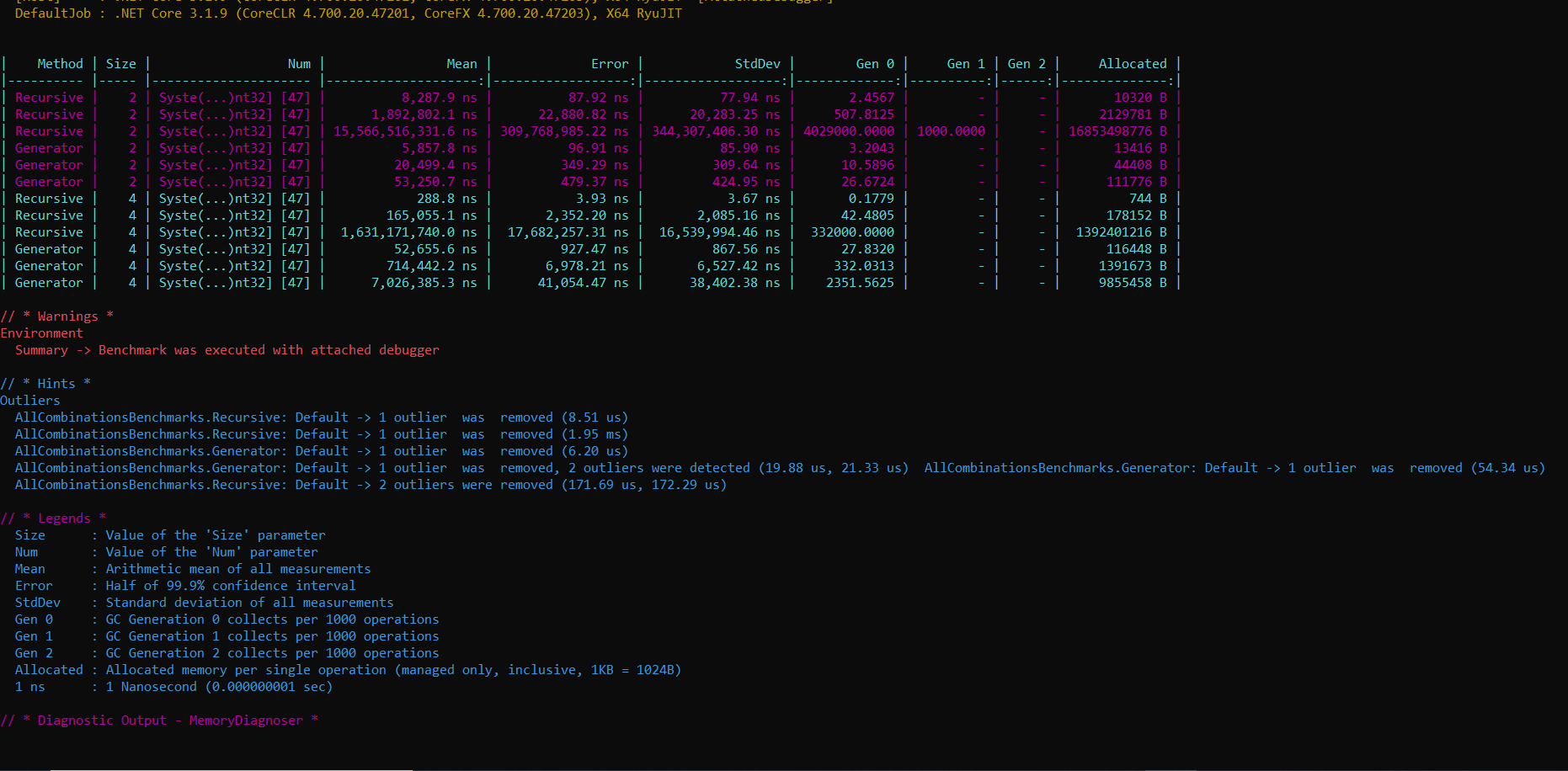
Its quite a dramatic difference especially when the dataset gets a little larger. Using an array of 11 items and a size of 4 takes 1.6 seconds recursively and 7 milliseconds with the index generator function. The memory usage is also 10,000 times bigger when using the recursive method. Yes, that most probably makes it worth me throwing away my fancy recursive method.